Quadratic Equations - Methods and Real-World Uses

Quadratic Equations – Essential Concepts and Practical Applications

Quadratic equations form a fundamental part of algebra, representing equations of the form: ax² + bx + c = 0. These equations appear frequently in various fields, from physics to engineering to economics, making their understanding crucial for solving many real-world problems. This guide will cover the essentials of quadratic equations, including their solutions, graphical representation, and practical applications.

Contents hide

Quadratic Equations – Essential Concepts and Practical Applications

What is a Quadratic Equation?

Solutions to Quadratic Equations

Factoring

Completing the Square

Quadratic Formula

Visualization: Quadratic Formula Solutions

Graphing Quadratic Equations

Key Features of Parabolas

Visualization: Graph of y = x2 – 4x + 3

Practical Applications of Quadratic Equations

Physics

Visualization: Projectile Motion

Economics

Visualization: Profit Maximization

Summary

What is a Quadratic Equation?

A quadratic equation is a second-degree polynomial equation in a single variable “x“, with the general form:

$ax^2 + bx + c = 0$

where:
– $a$ , $b$ , and $c$ are constants
– $$ a \neq 0 $ (if $ a = 0 $, the equation becomes linear)$

Solutions to Quadratic Equations

Quadratic equations can be solved using various methods, including factoring, completing the square, and the quadratic formula.

Factoring

Factoring involves expressing the quadratic equation as a product of two binomials. For example, consider the equation:

$x^2 - 5x + 6 = 0$

This can be factored as:

$(x - 2)(x - 3) = 0$

Setting each factor to zero gives the solutions:

$x - 2 = 0 \quad \Rightarrow \quad x = 2$

$x - 3 = 0 \quad \Rightarrow \quad x = 3$

Completing the Square

Completing the square transforms the quadratic equation into a perfect square trinomial. Consider the equation:

$x^2 + 6x + 5 = 0$

Rewrite the equation as:

$x^2 + 6x = -5$

Add and subtract $(6/2)^2 = 9$ on the left side:

$x^2 + 6x + 9 = -5 + 9$

This gives:

$(x + 3)^2 = 4$

Taking the square root of both sides:

$x + 3 = \pm 2$

Solving for $x$ :

$x = -3 \pm 2$

Thus, the solutions are:

$x = -1 \quad \text{and} \quad x = -5$

Quadratic Formula

The quadratic formula provides a straightforward way to find the roots of any quadratic equation:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

For example, consider the equation:

$2x^2 - 4x - 6 = 0$

Here, $a = 2$ , $b = -4$ , and $c = -6$ . Plugging these values into the quadratic formula gives:

$x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 \cdot 2 \cdot (-6)}}{2 \cdot 2}$

$x = \frac{4 \pm \sqrt{16 + 48}}{4}$

$x = \frac{4 \pm \sqrt{64}}{4}$

$x = \frac{4 \pm 8}{4}$

Thus, the solutions are:

$x = 3 \quad \text{and} \quad x = -1$

Visualization: Quadratic Formula Solutions

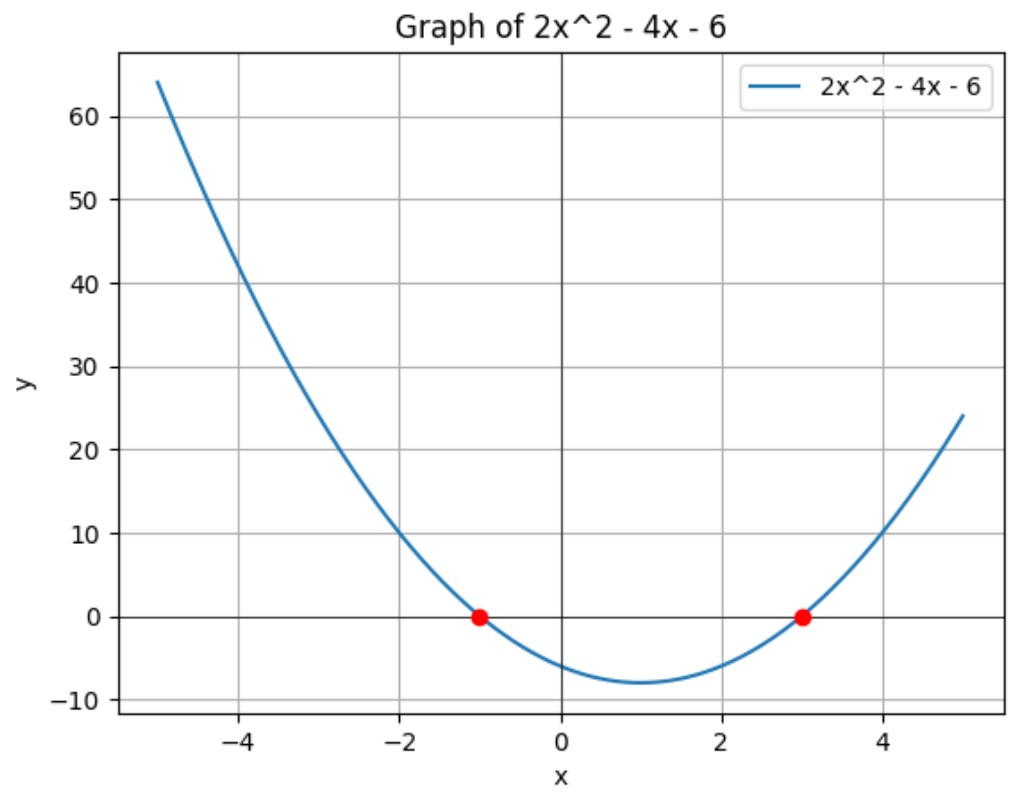
Graphing Quadratic Equations

Quadratic equations form parabolas when graphed.

The general shape is a “U” $(\text{if } $ a > 0 $) \text{or an upside-down "U" } (if $ a < 0 $)$ .

The vertex of the parabola represents the maximum or minimum value of the quadratic function.

Key Features of Parabolas

1. Vertex: The highest or lowest point on the graph, given by $\left(\frac{-b}{2a}, f\left(\frac{-b}{2a}\right)\right)$ .

2. Axis of Symmetry: The vertical line that passes through the vertex, given by $x = \frac{-b}{2a}$ .

3. Roots: The x-intercepts where the graph crosses the x-axis, found using the quadratic formula.

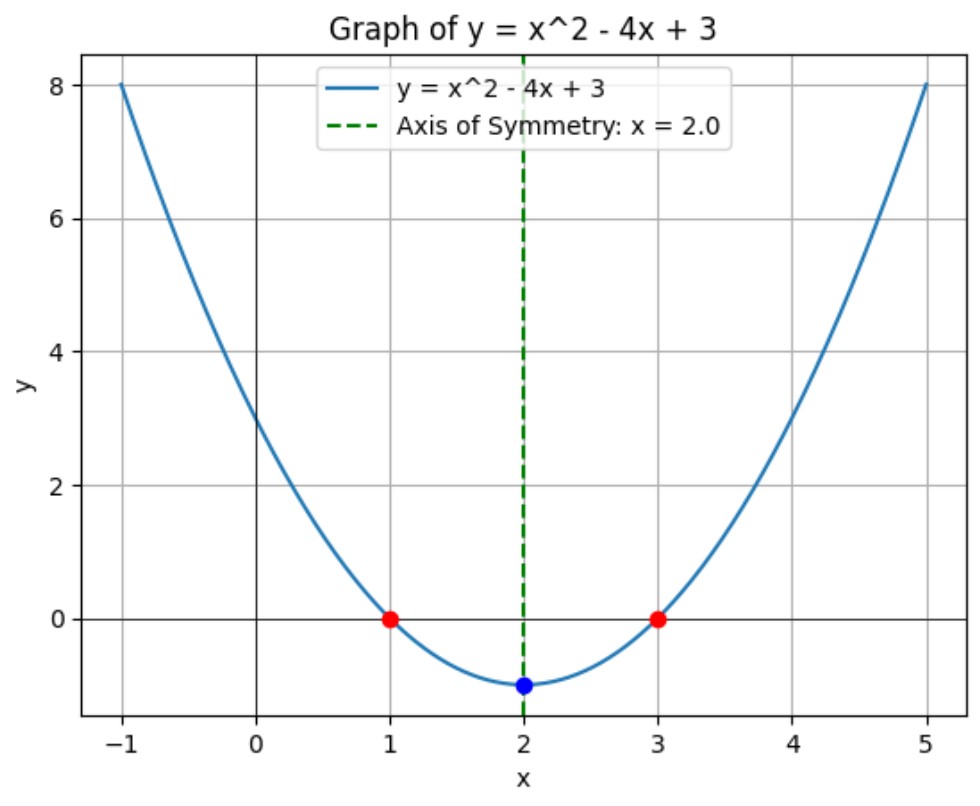
Example: Graphing $y = x^2 - 4x + 3$

1. Vertex: Calculate $x$ value using $x = \frac{-b}{2a}$ :

$x = \frac{-(-4)}{2(1)} = 2$

Calculate $y$ value at $x = 2$ :

$y = 2^2 - 4(2) + 3 = -1$

So, the vertex is $(2, -1)$ .

2. Axis of Symmetry: The line $x = 2$ .

3. Roots: Factor or use the quadratic formula to find $x$ :

$x^2 - 4x + 3 = 0 \quad \Rightarrow \quad (x - 1)(x - 3) = 0$

$x = 1 \quad \text{and} \quad x = 3$

Visualization: Graph of y = x² – 4x + 3

Practical Applications of Quadratic Equations

Quadratic equations appear in various real-world scenarios, often modeling situations where there is a maximum or minimum value.

Physics

In physics, quadratic equations model projectile motion. The height $y$ of an object at time $t$ can be given by:

$y = v_0 t - \frac{1}{2}gt^2$

where $v_0$ is the initial velocity and $g$ is the acceleration due to gravity. Solving this quadratic equation helps determine the maximum height reached by the object and the time it takes to hit the ground.

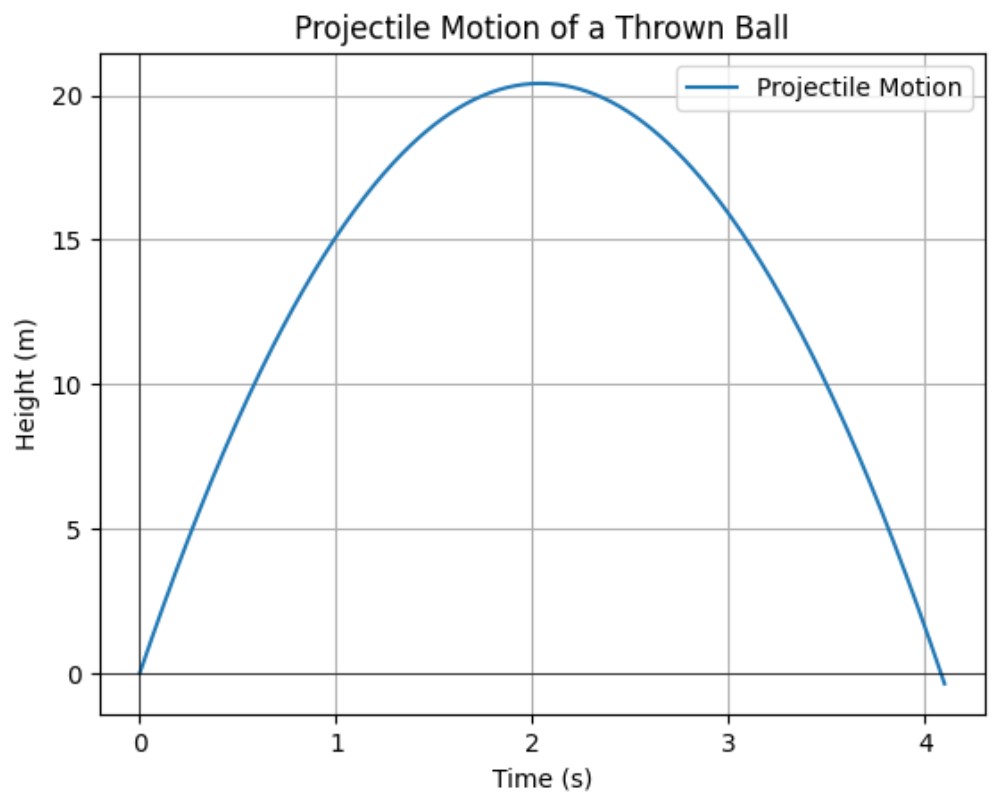
Example: Suppose a ball is thrown upwards with an initial velocity of 20 m/s. The height $y$ at time $t$ is given by:

$y = 20t - 5t^2$

Visualization: Projectile Motion

Economics

Quadratic equations can also model cost and revenue functions, helping businesses find the maximum profit.

Suppose a company’s revenue $R(x)$ and cost $C(x)$ functions are quadratic:

$R(x) = ax^2 + bx + c$

$C(x) = dx^2 + ex + f$

The profit $P(x)$ is given by the difference between revenue and cost:

$P(x) = R(x) - C(x)$

To maximize profit, we solve for $x$ by finding the vertex of the quadratic profit function.

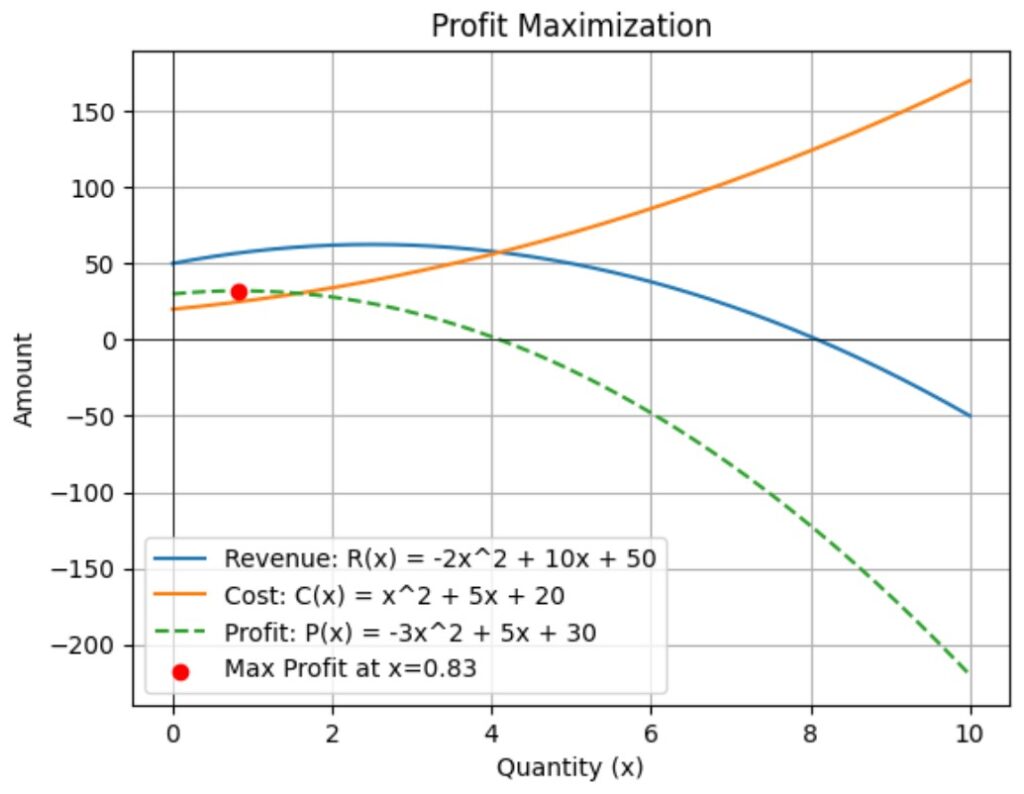
Example: Suppose the revenue function is $R(x) = -2x^2 + 10x + 50$ and the cost function is $C(x) = x^2 + 5x + 20$ . The profit function is:

$P(x) = (-2x^2 + 10x + 50) - (x^2 + 5x + 20)$

$P(x) = -3x^2 + 5x + 30$

To find the maximum profit, we determine the vertex of the profit function. The $x$ -coordinate of the vertex is given by $x = \frac{-b}{2a}$ :

$x = \frac{-5}{2(-3)} = \frac{5}{6}$

The maximum profit occurs at $x = \frac{5}{6}$ .

Visualization: Profit Maximization

Summary

Quadratic equations are powerful tools in mathematics, providing insights and solutions to a variety of real-world problems. Whether you’re working on projectile motion in physics, optimizing profit in business, or simply graphing parabolas, understanding how to solve and interpret quadratic equations is essential.

By mastering different methods of solving quadratic equations, such as factoring, completing the square, and using the quadratic formula, you can tackle a wide range of mathematical challenges. Graphing these equations helps visualize their behavior and identify key features like vertices, axes of symmetry, and roots.

In practical applications, quadratic equations are invaluable in modeling scenarios where there is a maximum or minimum value, making them crucial for decision-making in fields such as economics, engineering, and natural sciences.