Probability and Combinatorics – Essential Concepts and Applications
Probability and combinatorics are vital branches of mathematics that deal with the likelihood of events occurring and the various ways objects can be arranged or combined. Understanding these concepts is crucial in fields like statistics, computer science, and many everyday applications. This page covers key concepts in probability and combinatorics, providing clear explanations and practical examples to help you grasp these fundamental ideas.
Probability
Probability is the measure of the likelihood that an event will occur. It ranges from 0 to 1, where 0 indicates an impossible event and 1 indicates a certain event.
Basic Probability
The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
Example: If you roll a fair six-sided die, the probability of rolling a 4 is:
![\[ P(4) = \frac{1}{6} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-ee33317fd2f48e7aec4483395008d8cb_l3.png "Rendered by QuickLaTeX.com")
This is because there is only one favorable outcome (rolling a 4) out of six possible outcomes (1, 2, 3, 4, 5, 6).
Visualization: Basic Probability
Conditional Probability
Conditional probability is the probability of an event occurring given that another event has already occurred.
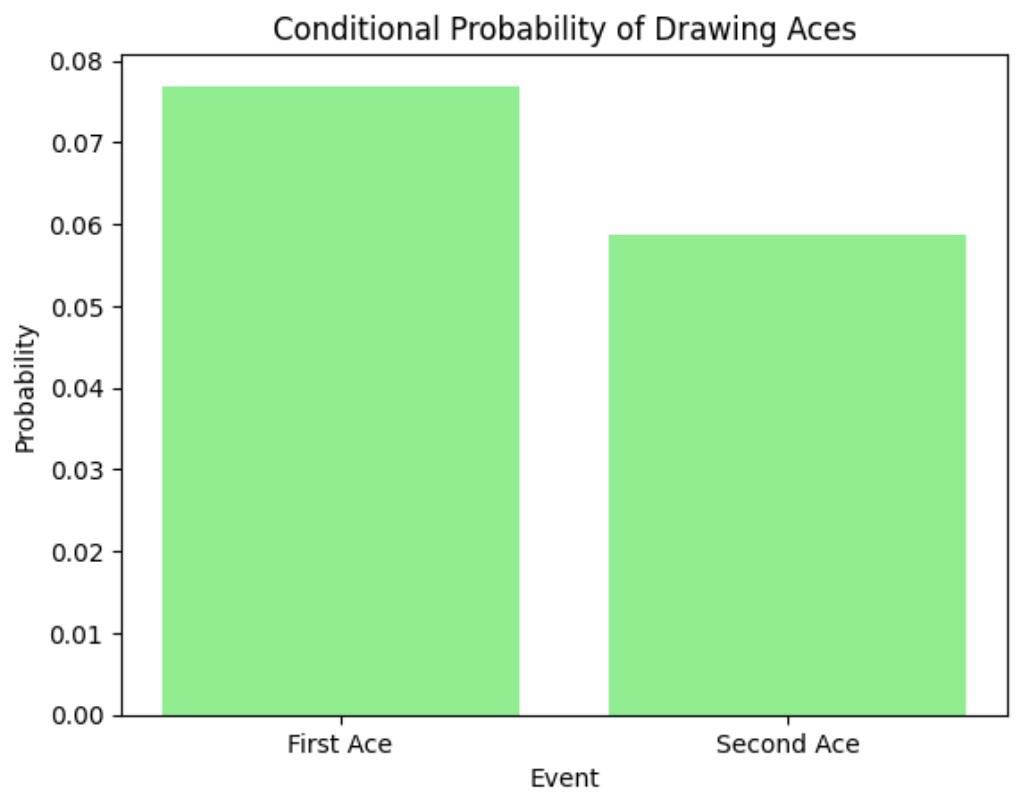
Example: If you draw a card from a deck of 52 cards, the probability of drawing an ace is:
![\[ P(Ace) = \frac{4}{52} = \frac{1}{13} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-24b2511e050a762a1e9b8a996f97afe5_l3.png "Rendered by QuickLaTeX.com")
If you draw another card without replacing the first, the probability of drawing another ace is:
![\[ P(Ace|Ace) = \frac{3}{51} = \frac{1}{17} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-33614b396d8caf871d563e2386219ea1_l3.png "Rendered by QuickLaTeX.com")
Visualization: Conditional Probability
Independent and Dependent Events
Events are independent if the outcome of one event does not affect the outcome of another. They are dependent if the outcome of one event affects the outcome of another.
Example: Rolling a die and flipping a coin are independent events because the result of the die roll does not affect the coin flip.
Example: Drawing cards from a deck without replacement is a dependent event because the outcome of one draw affects the outcomes of subsequent draws.
Combinatorics
Combinatorics is the branch of mathematics dealing with combinations, permutations, and the counting of objects. It helps in determining the number of ways objects can be arranged or combined.
Permutations
Permutations refer to the number of ways to arrange a set of objects where the order matters.
Example: Consider arranging the letters A, B, and C. The permutations are ABC, ACB, BAC, BCA, CAB, and CBA. There are 6 permutations.
The formula for permutations of 
objects is:
![\[ P(n) = n! \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-9a616b284a05c390e88fa78c051c89b6_l3.png "Rendered by QuickLaTeX.com")
Where 
(n factorial) is the product of all positive integers up to .
Visualization: Permutations
Combinations
Combinations refer to the number of ways to choose a subset of objects where the order does not matter.
Example: Choosing 2 letters from A, B, and C. The combinations are AB, AC, and BC. There are 3 combinations.
The formula for combinations of objects taken 
at a time is:
![\[ C(n, r) = \frac{n!}{r!(n-r)!} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-6281fb76be660320fc56e597ab29e690_l3.png "Rendered by QuickLaTeX.com")
Visualization: Combinations
Practical Applications of Probability and Combinatorics
Lottery Probability
Understanding probability helps in evaluating the odds of winning a lottery. For instance, the probability of winning a typical 6/49 lottery, where you must choose 6 numbers from a set of 49, is calculated as:
![\[ P(\text{win}) = \frac{1}{C(49, 6)} = \frac{1}{\frac{49!}{6!(49-6)!}} \approx \frac{1}{13,983,816} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-5b20e1fda19686375d9f1c90036ffdf1_l3.png "Rendered by QuickLaTeX.com")
This extremely low probability illustrates why winning the lottery is so rare.
Visualization: Lottery Probability
Combinatorial Optimization
Combinatorics plays a crucial role in optimization problems, such as the traveling salesman problem (TSP), where the goal is to find the shortest route that visits a set of cities and returns to the origin city.
Example: For 4 cities (A, B, C, D), the permutations representing different routes are:
- ABCD, ABDC, ACBD, ACDB, ADBC, ADCB
- BACD, BADC, BCAD, BCDA, BDAC, BDCA
- CABD, CADB, CBAD, CBDA, CDAB, CDBA
- DABC, DACB, DBAC, DBCA, DCAB, DCBA
By calculating the total distance for each route, the shortest path can be determined.
Wrapping It Up
Probability and combinatorics are fundamental mathematical concepts with numerous practical applications. By understanding and applying these principles, we can make informed decisions, solve complex problems, and better understand the world around us. Whether calculating the odds of an event, optimizing routes, or determining the number of possible combinations, mastering probability and combinatorics is essential for navigating a data-driven world.