Logarithms - From Basics to Real-World Applications

Logarithms – Key Concepts and Practical Applications

Logarithms are an essential mathematical concept used to solve equations involving exponential growth or decay. They are the inverse operations of exponentiation, allowing us to work with large numbers and exponential scales more easily. This page covers the basics of logarithms, their properties, and practical applications, providing detailed explanations and examples.

What Are Logarithms?

A logarithm answers the question: “To what exponent must a base number be raised, to produce a given number?”

For example, in the expression $\log_b(a) = c$ , $b^c = a$ . Here, $b$ is the base, $a$ is the argument, and $c$ is the logarithm.

Example:

If $\log_{10}(100) = 2$ , this means $10^2 = 100$ .

Common Logarithms and Natural Logarithms

Common Logarithms

Common logarithms use base 10 and are often written as $\log$ without specifying the base.

Example:

$$ \log(1000) = 3 $ because $ 10^3 = 1000 $.$

Natural Logarithms

Natural logarithms use base $e$ (approximately 2.71828) and are written as $\ln$ .

Example:

$$ \ln(e^2) = 2 $ because $ e^2 = e^2 $.$

Properties of Logarithms

Logarithms have several important properties that make them useful for simplifying complex calculations.

Product Property

$\log_b(xy) = \log_b(x) + \log_b(y)$

Example:

$$ \log_{10}(100 \cdot 10) = \log_{10}(100) + \log_{10}(10) = 2 + 1 = 3 $.$

Quotient Property

$\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)$

Example:

$$ \log_{10}\left(\frac{1000}{10}\right) = \log_{10}(1000) - \log_{10}(10) = 3 - 1 = 2 $.$

Power Property

$\log_b(x^y) = y \cdot \log_b(x)$

Example:

$$ \log_{10}(100^2) = 2 \cdot \log_{10}(100) = 2 \cdot 2 = 4 $.$

Change of Base Formula

$\log_b(a) = \frac{\log_c(a)}{\log_c(b)}$

Example:

$$ \log_2(8) = \frac{\log_{10}(8)}{\log_{10}(2)} \approx \frac{0.903}{0.301} \approx 3 $.$

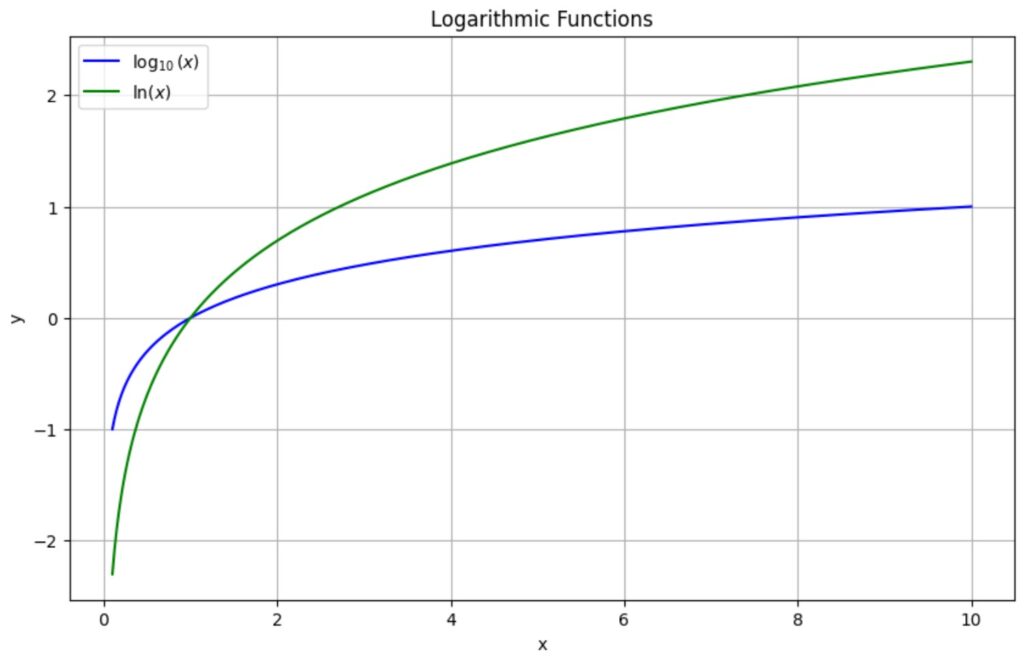
Graphs of Logarithmic Functions

Visualizing logarithmic functions helps in understanding their behavior.

Below is a graph of $\log_{10}(x)$ and $\ln(x)$ .

Visualization: Logarithmic Functions

Applications of Logarithms

Logarithms are widely used in various fields such as science, engineering, finance, and technology.

Exponential Growth and Decay

Logarithms help in solving equations related to exponential growth or decay, such as population growth, radioactive decay, and compound interest calculations.

Example:

If a population grows exponentially according to the formula $P(t) = P_0 e^{kt}$ where $P_0$ is the initial population, $k$ is the growth rate, and $t$ is time, we can find the time required for the population to double using logarithms.

Given $P(t) = 2P_0$ ,

$2P_0 = P_0 e^{kt}$

$2 = e^{kt}$

$\ln(2) = kt$

$t = \frac{\ln(2)}{k}$

Visualization: Exponential Growth

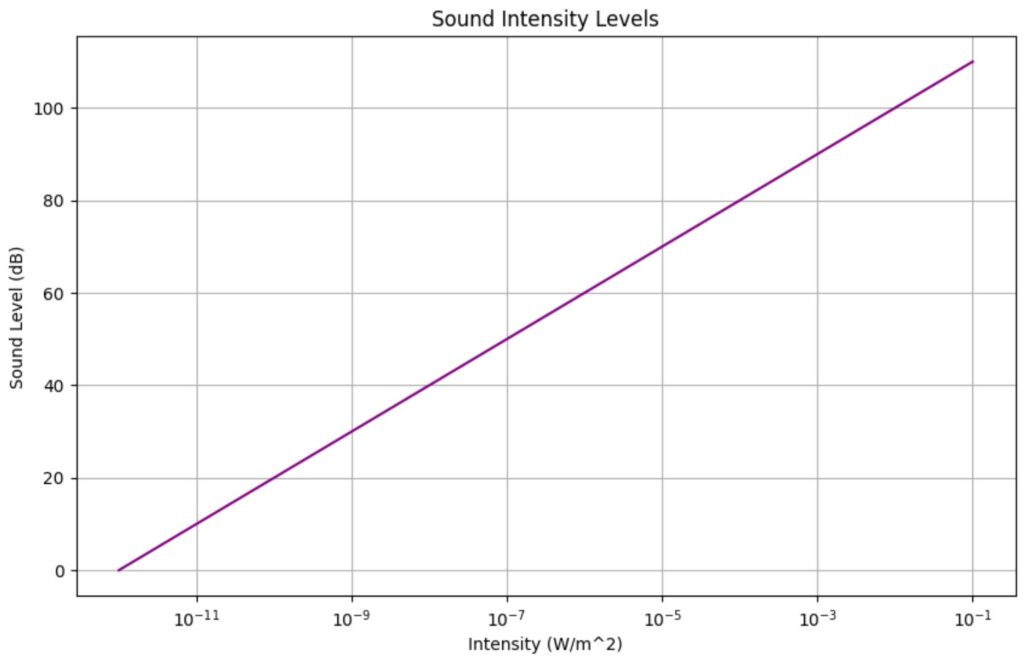
Acoustics and Sound Intensity

The decibel scale, used to measure sound intensity, is logarithmic. The sound intensity level $L$ in decibels is given by:

$L = 10 \log_{10}\left(\frac{I}{I_0}\right)$

where $I$ is the sound intensity and $I_0$ is the reference intensity.

Example:

If a sound has an intensity of $10^{-5}$ watts per square meter and the reference intensity is $10^{-12}$ watts per square meter,

$L = 10 \log_{10}\left(\frac{10^{-5}}{10^{-12}}\right) = 10 \log_{10}(10^7) = 10 \cdot 7 = 70 \text{ dB}$

Visualization: Sound Intensity

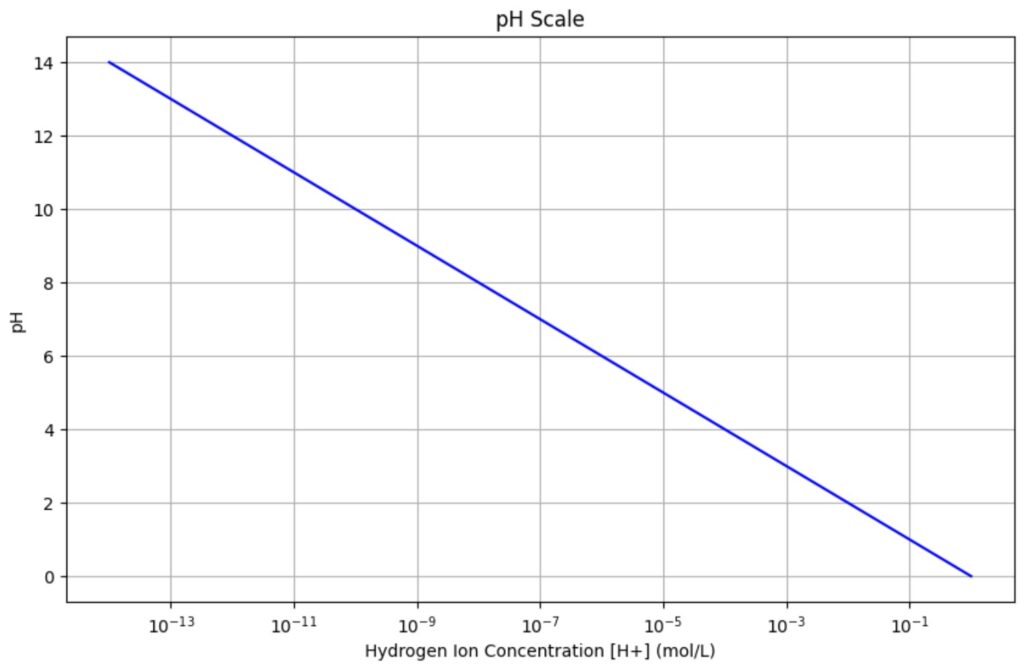
pH Scale in Chemistry

The pH scale, which measures the acidity or alkalinity of a solution, is logarithmic. The pH is defined as:

$\text{pH} = -\log_{10}[H^+]$

where $[H^+]$ is the concentration of hydrogen ions in moles per liter.

Example:

If the hydrogen ion concentration of a solution is $10^{-4}$ moles per liter,

$\text{pH} = -\log_{10}(10^{-4}) = 4$

Visualization: pH Scale

Conclusion

Logarithms are a fundamental concept in mathematics with a wide range of applications. From solving exponential growth and decay problems to measuring sound intensity and acidity, logarithms provide powerful tools for handling complex calculations. Understanding their properties and applications can greatly enhance your problem-solving skills and comprehension of various scientific and mathematical phenomena.