Financial Mathematics

Financial Mathematics – Key Concepts and Applications

Financial mathematics is a crucial field that combines mathematical methods with financial theory to solve problems in finance. It includes a wide range of topics, from simple interest calculations to complex models for assessing financial risk. This page provides a comprehensive guide to key concepts in financial mathematics, complete with detailed explanations and practical examples.

Contents hide
Financial Mathematics – Key Concepts and Applications
Simple Interest
Visualization: Simple Interest
Compound Interest
Visualization: Compound Interest
Annuities
Visualization: Annuities
Amortization
Visualization: Amortization
Bonds
Visualization: Bond Price
Wrapping It Up

Simple Interest

Simple interest is the easiest type of interest calculation. It is calculated using the formula:

    \[ \text{Simple Interest} = P \times r \times t \]

where \( P \) is the principal amount, \( r \) is the annual interest rate, and \( t \) is the time in years.

Example: If you deposit $1,000 in a savings account with an annual interest rate of 5% for 3 years, the simple interest earned is:

    \[ \text{Simple Interest} = 1000 \times 0.05 \times 3 = 150 \]

Visualization: Simple Interest

Compound Interest

Compound interest is calculated on the initial principal and also on the accumulated interest of previous periods. The formula for compound interest is:

    \[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]

where \( A \) is the amount of money accumulated after \( n \) years, including interest, \( P \) is the principal amount, \( r \) is the annual interest rate, \( n \) is the number of times that interest is compounded per year, and \( t \) is the time the money is invested for in years.

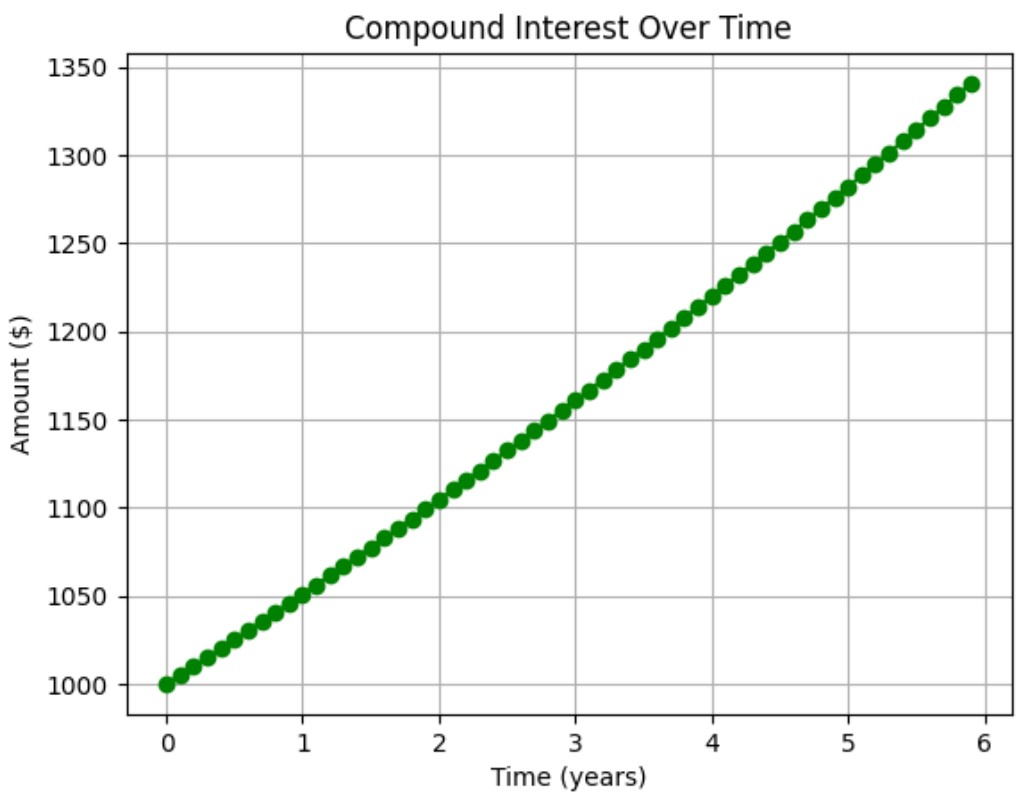
Example: If you invest $1,000 at an annual interest rate of 5% compounded quarterly for 3 years, the future value is:

    \[ A = 1000 \left(1 + \frac{0.05}{4}\right)^{4 \times 3} \approx 1161.62 \]

Visualization: Compound Interest

Annuities

An annuity is a series of equal payments made at regular intervals. The future value of an annuity is calculated using the formula:

    \[ FV = PMT \times \frac{(1 + r)^n - 1}{r} \]

where \( PMT \) is the payment amount, \( r \) is the interest rate per period, and \( n \) is the number of payments.

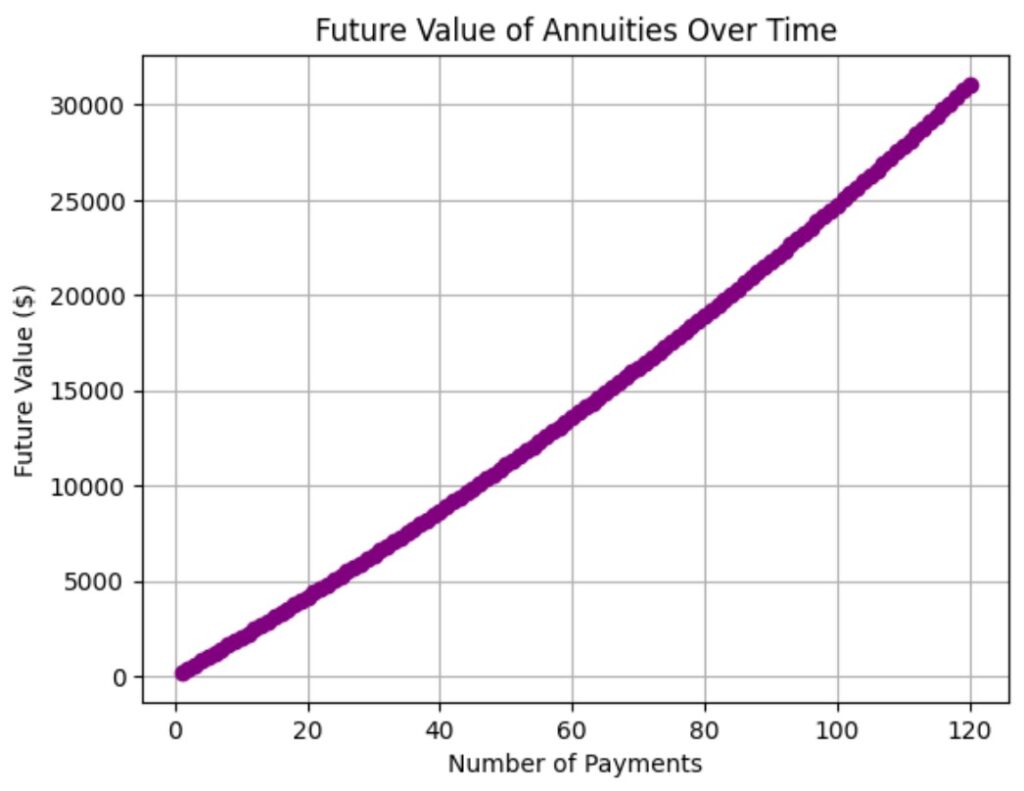
Example: If you make monthly deposits of $200 into an account that earns 5% annual interest, compounded monthly, for 10 years, the future value of the annuity is:

    \[ FV = 200 \times \frac{(1 + 0.00417)^{120} - 1}{0.00417} \approx 30,528.51 \]

Visualization: Annuities

Amortization

Amortization is the process of spreading out a loan into a series of fixed payments over time. The monthly payment on an amortized loan is calculated using the formula:

    \[ PMT = P \times \frac{r(1 + r)^n}{(1 + r)^n - 1} \]

where \( PMT \) is the monthly payment, \( P \) is the principal amount, \( r \) is the monthly interest rate, and \( n \) is the number of payments.

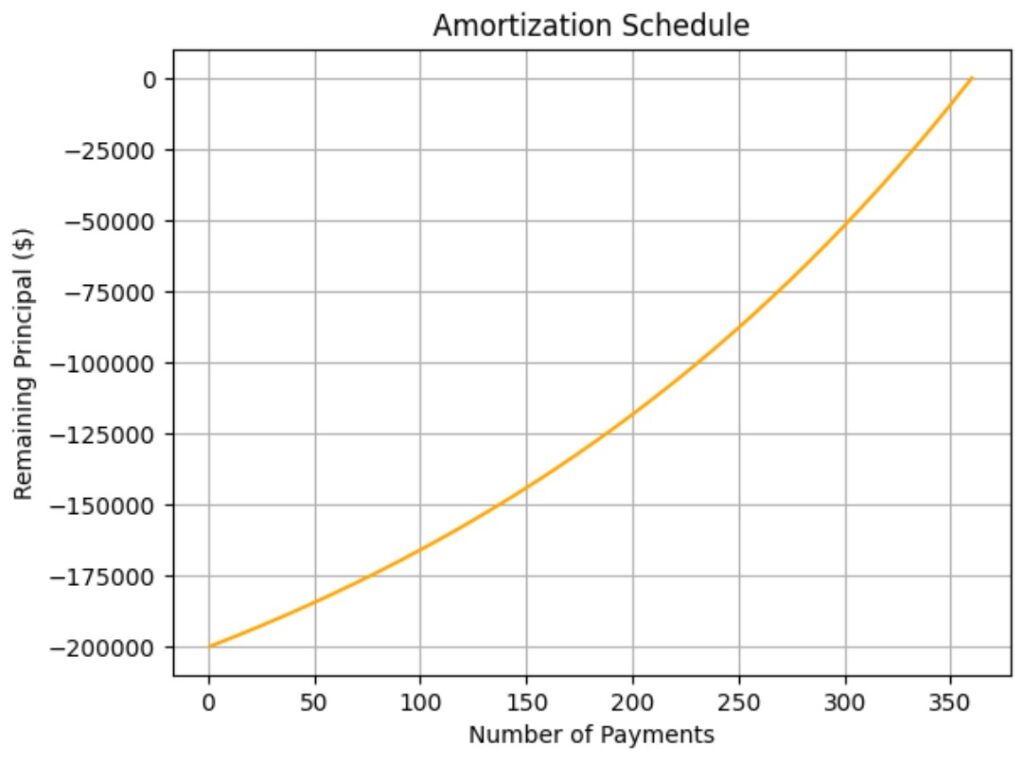
Example: For a $200,000 mortgage at a 4% annual interest rate (0.33% monthly) over 30 years (360 payments), the monthly payment is:

    \[ PMT = 200000 \times \frac{0.00333(1 + 0.00333)^{360}}{(1 + 0.00333)^{360} - 1} \approx 954.83 \]

Visualization: Amortization

Bonds

A bond is a fixed income instrument that represents a loan made by an investor to a borrower. The price of a bond can be calculated using the present value of its future coupon payments and the face value at maturity.

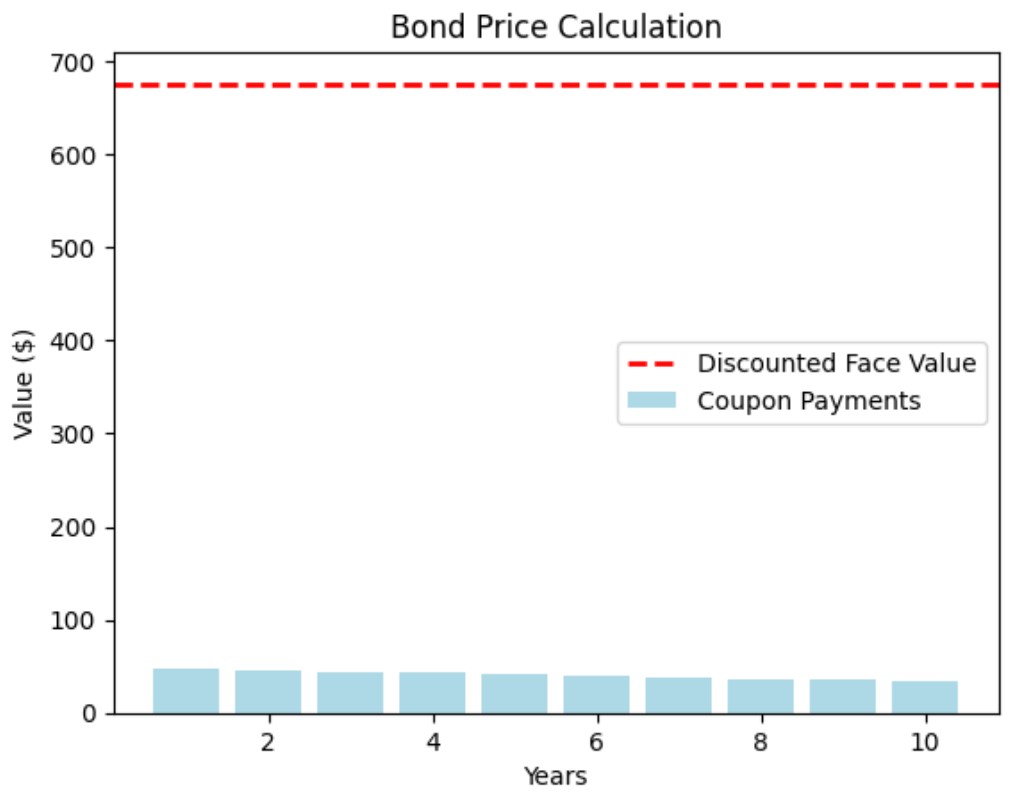
Example: Consider a bond with a face value of $1,000, a coupon rate of 5%, and a maturity of 10 years. If the market interest rate is 4%, the price of the bond can be calculated by discounting the future cash flows.

    \[ \text{Bond Price} = \sum \left(\frac{C}{(1 + r)^t}\right) + \frac{F}{(1 + r)^n} \]

where \( C \) is the coupon payment, \( r \) is the market interest rate, \( t \) is the time period, \( F \) is the face value, and \( n \) is the number of periods.

Visualization: Bond Price

Wrapping It Up

Financial mathematics is a vital discipline that helps individuals and organizations make informed decisions regarding money. By understanding concepts like simple and compound interest, annuities, amortization, and bonds, you can effectively manage finances and assess financial instruments. Through the use of visualizations, these concepts become clearer and more accessible, aiding in the practical application of financial mathematics in everyday life.