Basic Trigonometry – Key Principles and Real-World Uses
Trigonometry is a branch of mathematics that studies relationships between the angles and sides of triangles. It has numerous applications in fields such as physics, engineering, astronomy, and even in everyday tasks like navigation and architecture. This page will provide an in-depth guide to the fundamental concepts of trigonometry, using detailed explanations and practical examples to illustrate key principles.
The Trigonometric Ratios
At the heart of trigonometry are the trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). These ratios are defined for a right-angled triangle and are used to relate the angles to the lengths of the sides.
Sine (sin)
The sine of an angle in a right triangle is the ratio of the length of the opposite side to the length of the hypotenuse.
![\[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-611ae273764c7d7dedf294803287fd2e_l3.png "Rendered by QuickLaTeX.com")
Cosine (cos)
The cosine of an angle in a right triangle is the ratio of the length of the adjacent side to the length of the hypotenuse.
![\[ \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-a913422767ccdf457eef93d86edbc17c_l3.png "Rendered by QuickLaTeX.com")
Tangent (tan)
The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side.
![\[ \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-8e91beae17fab88d238b79c20d5903df_l3.png "Rendered by QuickLaTeX.com")
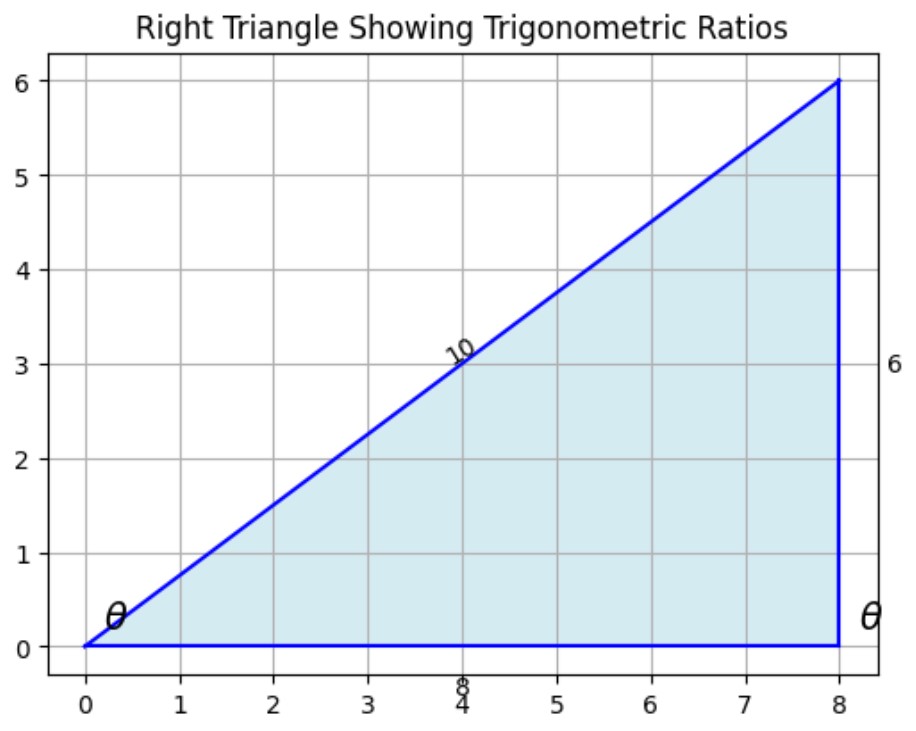
Example: Right Triangle
Consider a right triangle with a hypotenuse of 10 units, an opposite side of 6 units, and an adjacent side of 8 units. Let’s calculate the sine, cosine, and tangent for the angle θ opposite the 6-unit side.
![\[ \sin(\theta) = \frac{6}{10} = 0.6 \] \[ \cos(\theta) = \frac{8}{10} = 0.8 \] \[ \tan(\theta) = \frac{6}{8} = 0.75 \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-1222879c82e258e0054178fd98baff92_l3.png "Rendered by QuickLaTeX.com")
Visualization of Trigonometric Ratios
A right triangle can visually demonstrate these trigonometric ratios.
The Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of a coordinate plane. It is a powerful tool in trigonometry because it provides a way to define trigonometric functions for all angles.
Unit Circle Definitions
- Sine of an angle is the y-coordinate of the point where the terminal side of the angle intersects the unit circle.
- Cosine of an angle is the x-coordinate of this point.
- Tangent of an angle is the y-coordinate divided by the x-coordinate of this point.
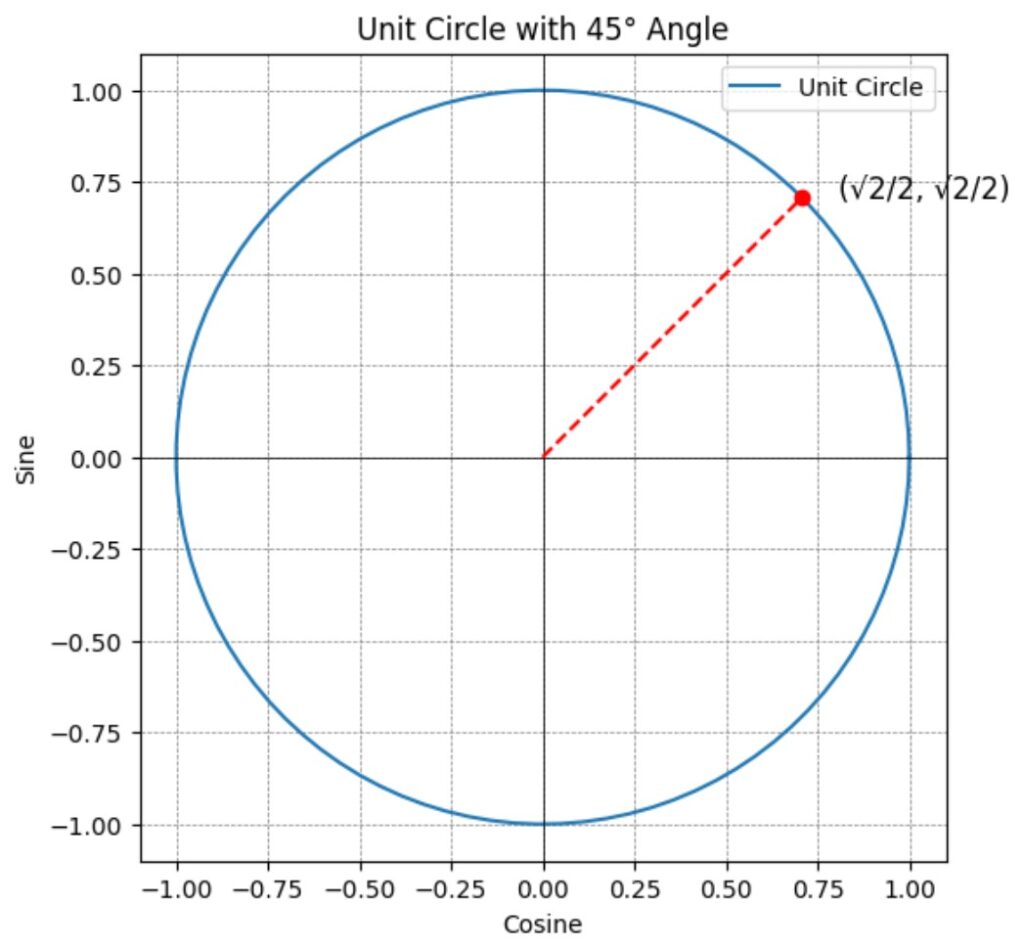
Example: Unit Circle
Consider an angle of 45° (or π/4 radians). The point on the unit circle at this angle has coordinates (√2/2, √2/2).
![\[ \sin(45^\circ) = \frac{\sqrt{2}}{2} \] \[ \cos(45^\circ) = \frac{\sqrt{2}}{2} \] \[ \tan(45^\circ) = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \]](https://hozaki.com/wp-content/ql-cache/quicklatex.com-fd6088f88d838c857b5dee6fe34daf90_l3.png "Rendered by QuickLaTeX.com")
Visualization of the Unit Circle
The unit circle can visually demonstrate the values of sine and cosine for various angles.
Applications of Trigonometry
Trigonometry is not just an abstract mathematical concept; it has numerous practical applications:
Architecture and Engineering
Trigonometry is essential in designing and constructing buildings, bridges, and other structures. Engineers use trigonometric functions to calculate forces, angles, and distances, ensuring structural integrity and stability.
Navigators use trigonometry to determine their position and chart courses. By measuring angles between known landmarks or celestial bodies, they can calculate distances and plot accurate routes.
Physics
In physics, trigonometry is used to analyze wave patterns, describe oscillatory motion, and solve problems involving vectors. It helps in understanding phenomena like sound waves, light waves, and electromagnetic fields.
Art and Graphics
Artists and graphic designers use trigonometry to create accurate perspectives and proportions. It aids in rendering three-dimensional objects on two-dimensional surfaces, making artwork more realistic.
Wrapping It Up
Basic trigonometry provides the foundation for understanding and solving problems involving angles and distances. By mastering the trigonometric ratios, the unit circle, and their applications, you gain valuable tools that are widely used in science, engineering, navigation, and art. Whether you’re calculating the height of a building or designing a bridge, trigonometry offers precise methods for making accurate measurements and informed decisions.